Cone Shape

Geometrical Stiffness of Loudspeaker Cones

A FINECone FEM Study by Peter Larsen, LOUDSOFT Copenhagen, Denmark

Abstract: The frequency response of a loudspeaker cone is affected by two main factors: Material Parameters and Geometry. While the first may be generally understood, the inherent stiffness due to the basic geometry is the subject of this study.

Using Finite Element Modelling (FEM), first a flat cone disk is analysed followed by shallow and deep conical cones plus curved concave and convex cones. The results are extended to include softer and high damping cone materials. The cone break-up behaviour and frequency response is shown to be strongly dependant on the Geometrical Stiffness of the Cone, which should therefore be considered a very important design parameter.

This study will use a 6.5” woofer from the FINECone Tutorial example, which is a realistic model with a rubber surround, spider and voice coil/former modelled with actual impedance. The FEM is made using FINECone, which is a FEM software package based on the axi-symmetric Multi Segment Method [3].

We will only change the shape of the cone. However since a large dust cap can influence the cone behaviour a lot, the diameter of the dust cap is reduced to that of the voice coil. The cone material is aluminium, because the cone modes here are evident and almost undamped. For clarity let us start with a completely flat cone (disk).

The frequency response of the completely flat cone is shown in Fig. 1. The upper curve (black) is the on axis response and the middle (blue) is 30 degree off-axis, and lower (red) is 60 degree off-axis. The response is irregular already from 100 Hz due to break-up, because the geometrical stiffness is low despite the use of the stiff aluminium material.

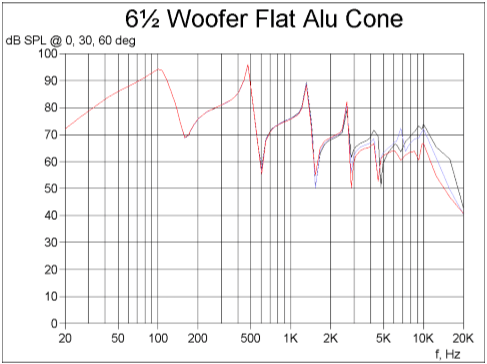
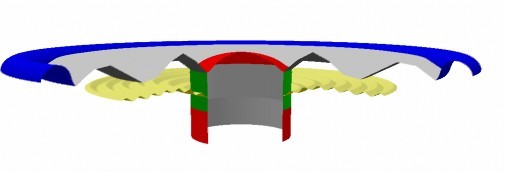
Figure 1. The frequency response of the completely flat cone is irregular already from 100 Hz

A high order break-up mode with several node lines is illustrated in Fig. 2. Due to the decreasing wavelength, the break-up is closing in towards the centre and has just reached the voice coil for the shown mode at 2868Hz.

Figure 2. 3D plot of Mode at 2868Hz

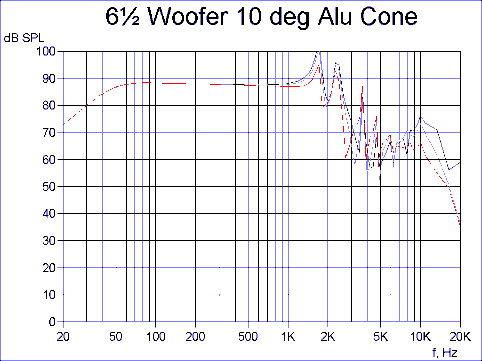
Now we go to a conical almost flat cone, having a cone angle of only 10 degrees from flat, see Fig.3. The frequency response is dramatically improved due to the slightly conical cone having considerably more (geometrical) stiffness in the vertical direction.

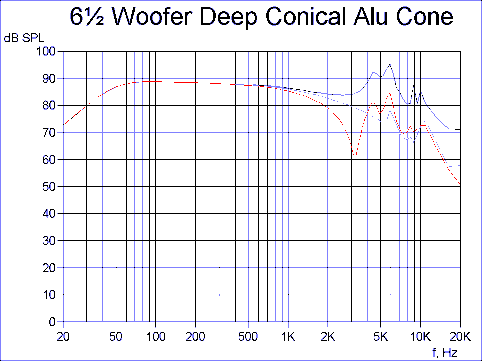
Figure 3. The frequency response of the 10-degree cone is flat up to 1000Hz.

Since the shallow 10 degree cone changed the break-up pattern considerably, let us then examine a more normal deep conical cone in comparison.

Fig. 4. The deep conical cone has extended response, but still some moderate peak(s) at high frequencies. This is quite typical for the conical cone regardless of material.

Figure 4. The deep conical cone has extended response, with moderate peak(s) at high frequencies .

Curving the cone is known to have a large effect on the response. Let us therefore examine the curved cone shown in fig. 5.

Figure 5. Deep curved Alu Cone Geometry

Figure 6. The frequency response of th e curved cone is extended at high frequencies, but with a small peak followed by a step and a “hole”.

The simulated frequency response of the curved cone from Fig. 5 is shown in fig. 6, and is now very extended at high frequencies, but unfortunately with a small peak followed by a step and “hole” already at 1500 Hz.

The 3D plot in Fig. 7 of the mode at 1700 Hz reveals that the outer edge of the cone + surround is breaking up and moving out of phase with the main part of the cone above 1700 Hz. This behaviour is causing the well-known “Edge hole” due to lack of geometrical stiffness along the flat cone edge.

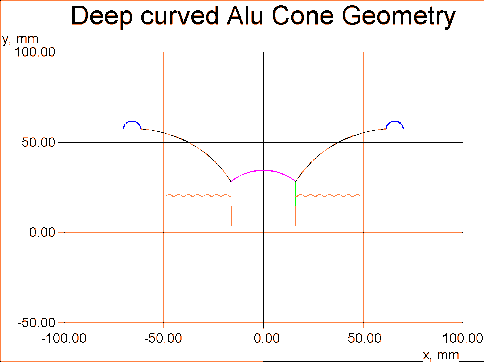
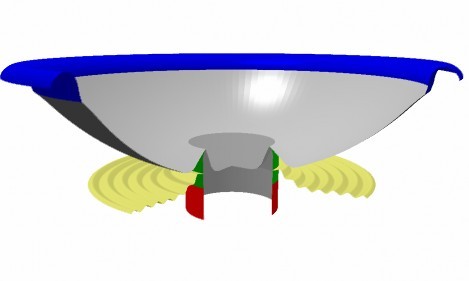
Figure 7. 3D Plot of curved cone mode at 1700 Hz. Flexing seen along edge.

In contrast let us therefore analyse the opposite: a concave curved cone having the same depth as before, see Fig. 9.

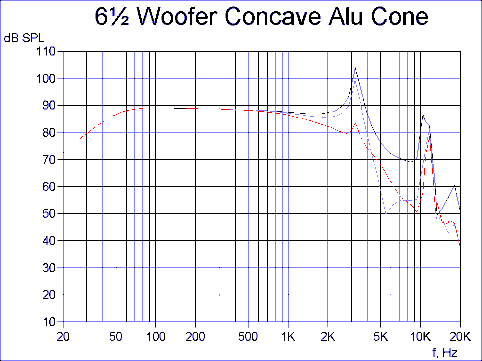
Fig. 8 shows that the concave curved cone has a flat response up to a higher frequency but with more pronounced peaks

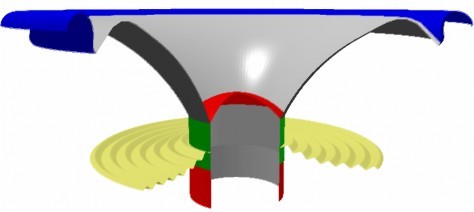
Figure 8. The concave curved cone has extended response with large peaks.

Here the conditions are reversed, see 3D plot of mode at 3193 Hz in Fig. 9. There is no problem along the edge, but the (inside) cone neck is bending, causing big peaks above 3 and 10 kHz, which is the effect of reduced geometrical stiffness at the neck.

Figure 9. 3D plot of concave curved cone mode at 3193 Hz. Flexing seen at voice coil neck.

We may increase the neck stiffness by bending the cone neck. Fig. 10 shows such an example Y-cone.

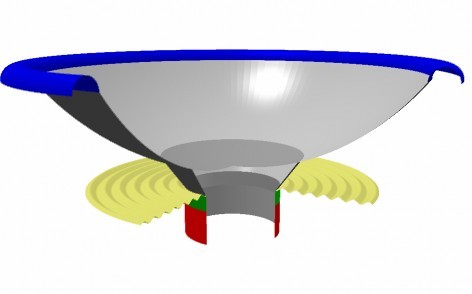
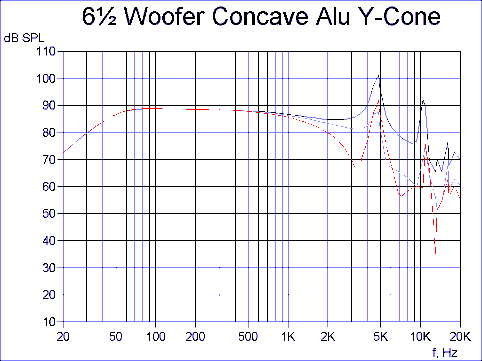
Figure 10. Concave curved cone geometry with bended cone neck (Y-cone)

Fig. 11 shows the response of the Y-cone. Basically we see the same response shape as before, however with the lower peak now moved up to 5kHz. This is due to increased geometrical stiffness along the voice coil neck.

Figure 11. Response of concave curved cone with bended cone neck (Y-cone ). The lower peak is moved up to 5 kHz

Soft and High Damping Cone Materials

In the previous section I have considered aluminium cones only, mainly due to their very limited damping characteristics. In this section I will analyse other materials applied to two of the earlier cases. It is important to realise that the use of a soft cone material with a geometry having little geometrical stiffness is usually not a good idea, because the reduced stiffness will inevitably worsen the problems caused by break-up. As a consequence I will analyse the previous concave Y-cone using talc filled PP-material.

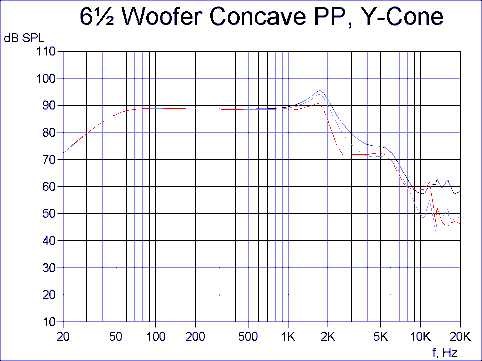
Figure 12. Response of concave curved PP-cone with bended cone neck (Y-cone). The response shape is approximately 2nd order Low Pass.

From Fig. 12 it can be seen that the response is remarkable having an approximate low pass shape above 2 kHz. The peak here was shifted down in frequency due to the lower stiffness of PP compared to aluminium, but well damped because of much higher damping in the PP material. In the last example the previous deep conical cone is analysed using a medium stiff paper pulp with high damping.

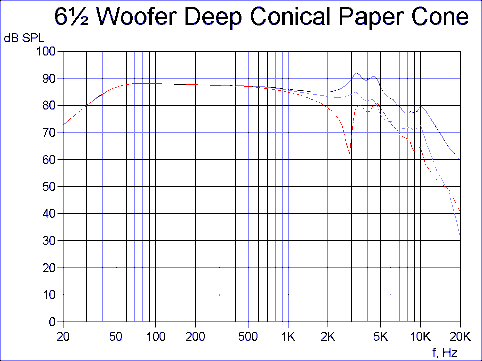
Figure 13. Response of deep conical paper cone. Smooth with moderate peaks.

The response of the deep conical paper cone is shown as Fig. 13 and is well behaved and smoother than the aluminium cone. Note the 3-4 kHz peaks are moved down in frequency due to the lower stiffness of the used paper compared to aluminium, but well damped because of much higher damping.

Conclusion
The cone break-up behaviour and frequency response was shown to be strongly dependant on the Geometrical Stiffness of the Cone, which should therefore be considered a very important design parameter.

Further it may be concluded that cone materials like soft paper; Kevlar and PP will normally have lower stiffness and are therefore best used in designs having high geometrical stiffness.

Presented by Peter Larsen at the 2003 ALMA World Cone Symposium